Exemplo De Equação Do 2 Grau, também conhecida como equação quadrática, é um conceito fundamental na matemática, presente em diversas áreas do conhecimento e da vida cotidiana. Essas equações, que se caracterizam por possuírem um termo de segundo grau, são ferramentas poderosas para modelar e resolver problemas que envolvem relações não lineares.
Desde o cálculo de trajetórias de projéteis na física até a otimização de custos em economia, as equações do 2º grau permeiam áreas como engenharia, biologia, e até mesmo a arquitetura. Compreender seus fundamentos e métodos de resolução é essencial para desvendar os mistérios por trás de diversos fenômenos e aplicações práticas.
Equações do 2º Grau: Uma Introdução
As equações do 2º grau são um conceito fundamental na matemática, com aplicações que se estendem além do âmbito acadêmico, impactando diversas áreas do conhecimento e da vida prática. Essas equações, caracterizadas por um termo de segundo grau, representam um tipo específico de relação matemática que permite modelar e solucionar problemas em diferentes contextos.
Em termos simples, uma equação do 2º grau é uma equação polinomial que possui um termo com a variável elevada ao quadrado (x²). A importância dessas equações reside na sua capacidade de descrever e resolver problemas que envolvem relações quadráticas, como a trajetória de um projétil, o crescimento de uma população ou a otimização de um projeto de engenharia.
Aplicações do Mundo Real
As equações do 2º grau são ferramentas essenciais para modelar e resolver problemas reais em diversas áreas, como:
- Física:O movimento de projéteis, a queda livre de objetos e a trajetória de um satélite podem ser descritos por equações do 2º grau.
- Engenharia:O cálculo de estruturas, a otimização de projetos e a modelagem de sistemas mecânicos frequentemente se baseiam em equações do 2º grau.
- Economia:A modelagem de custos, lucros e a análise de mercados financeiros utilizam equações do 2º grau para prever tendências e tomar decisões estratégicas.
- Biologia:O crescimento populacional, a dinâmica de ecossistemas e a modelagem de processos biológicos podem ser descritos por equações do 2º grau.
Estrutura da Equação do 2º Grau: Exemplo De Equação Do 2 Grau
A forma geral de uma equação do 2º grau é dada por:
ax² + bx + c = 0
onde:
- a, be csão coeficientes reais, sendo adiferente de zero (a ≠ 0).
- xé a variável.
Os coeficientes a, be cdesempenham um papel crucial na forma da parábola que representa a equação do 2º grau. O coeficiente adetermina a concavidade da parábola (para cima se a> 0 e para baixo se a < 0). O coeficiente binfluencia a posição da parábola no eixo horizontal, enquanto o coeficiente cdetermina o ponto de intersecção da parábola com o eixo vertical (o ponto onde x= 0).
Exemplos de Equações do 2º Grau
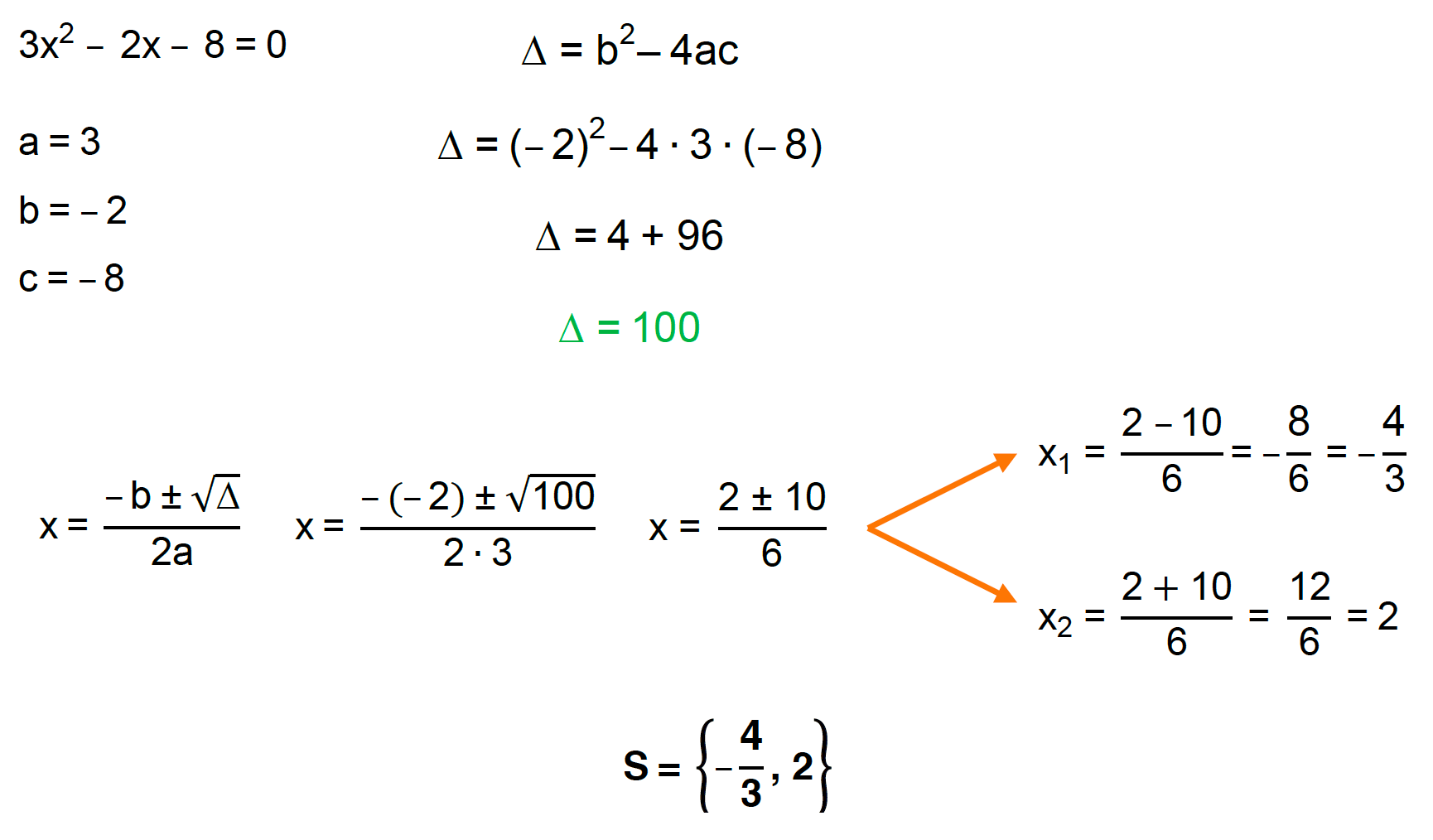
Para ilustrar a influência dos coeficientes na forma da parábola, observe os exemplos a seguir:
- x² + 2x- 3 = 0 : Nesta equação, a= 1, b= 2 e c= -3. A parábola é voltada para cima ( a> 0), com o vértice localizado no ponto (-1, -4). A parábola intercepta o eixo vertical no ponto (0, -3).
- -2x² + 4x- 1 = 0 : Nesta equação, a= -2, b= 4 e c= -1. A parábola é voltada para baixo ( a < 0), com o vértice localizado no ponto (1, 1). A parábola intercepta o eixo vertical no ponto (0, -1).
Métodos de Resolução
Existem vários métodos para resolver equações do 2º grau, cada um com suas vantagens e desvantagens. Os métodos mais comuns são:
| Método | Descrição | Passos | Exemplo |
|---|---|---|---|
| Fórmula de Bhaskara | A fórmula de Bhaskara é uma fórmula geral que fornece as raízes da equação do 2º grau, independentemente dos valores dos coeficientes. | 1. Identifique os valores de a, b e c na equação.
2. Substitua os valores na fórmula de Bhaskara
|
x² + 2x
a = 1, b = 2, c =
x = (-2 ± √(2²
x = (-2 ± √(16)) / 2×1 = 1 e x2 =
|
| Fatoração | A fatoração consiste em transformar a equação do 2º grau em um produto de dois fatores lineares. | 1. Encontre dois números que, quando multiplicados, resultam em ace, quando somados, resultam em b.
|
x² + 2x
(x + 3)(x
x + 3 = 0 ou x
x1 =
|
| Completando o Quadrado | O método de completar o quadrado consiste em manipular a equação do 2º grau para transformá-la em um quadrado perfeito. | 1. Divida ambos os lados da equação por a.
|
x² + 2x
x² + 2x = 3x² + 2x + 1 = 3 + 1(x + 1)² = 4x + 1 = ±2×1 = 1 e x2 =
|
Discriminante e Natureza das Raízes

O discriminante (Δ) da equação do 2º grau é dado por:
Δ = b²
4ac
O discriminante fornece informações sobre a natureza das raízes da equação do 2º grau, ou seja, quantos e quais tipos de soluções a equação possui.
- Δ > 0: A equação possui duas raízes reais e distintas. Isso significa que a parábola intercepta o eixo horizontal em dois pontos distintos.
- Δ = 0: A equação possui duas raízes reais e iguais (raiz dupla). Isso significa que a parábola intercepta o eixo horizontal em um único ponto, o vértice da parábola.
- Δ < 0: A equação possui duas raízes complexas conjugadas. Isso significa que a parábola não intercepta o eixo horizontal, ou seja, não possui raízes reais.
Exemplos de Equações com Diferentes Discriminantes
- x² + 2x- 3 = 0 : Δ = 2² – 4 – 1 – -3 = 16 > 0. A equação possui duas raízes reais e distintas: x1 = 1 e x2 = -3.
- x²- 4x + 4 = 0 : Δ = (-4)² – 4 – 1 – 4 = 0. A equação possui duas raízes reais e iguais: x1 = x2 = 2.
- x² + 2x + 2 = 0: Δ = 2² – 4 – 1 – 2 = -4 < 0. A equação possui duas raízes complexas conjugadas: x1 = -1 + i e x2 = -1 - i.
Commonly Asked Questions
Quais são as aplicações práticas da equação do 2º grau?
As equações do 2º grau possuem diversas aplicações práticas, como: calcular a trajetória de um projétil, determinar o ponto de equilíbrio em um mercado, modelar o crescimento populacional de uma espécie, entre outros.
Por que a equação do 2º grau é importante?
A equação do 2º grau é importante porque permite modelar e resolver problemas que envolvem relações não lineares, que são comuns em diversas áreas do conhecimento, como física, engenharia, economia e biologia.
Como posso saber se uma equação é do 2º grau?
Uma equação é do 2º grau se possui um termo com a variável elevada ao quadrado. A forma geral da equação do 2º grau é ax² + bx + c = 0, onde a, b e c são coeficientes.

