Calculo De Area Perimetro E Volume Com Exemplo Para Imprimir: Já imaginou construir uma casa sem saber quanto cimento vai precisar? Ou pintar uma parede sem calcular a tinta? A matemática, meu amigo, entra em cena! Esse guia vai te mostrar, de forma simples e divertida, como calcular áreas, perímetros e volumes, com exemplos práticos que você pode imprimir e usar na hora que precisar.
Prepare-se para dominar essas ferramentas essenciais e se tornar um mestre da medida!
Vamos mergulhar no mundo das formas geométricas, desde o quadrado mais básico até o cone mais desafiador. Aprenderemos as fórmulas mágicas para calcular a área de um terreno, o perímetro de uma piscina ou o volume de um tanque de combustível. Com exemplos práticos e passo a passo, você vai entender cada cálculo como se estivesse construindo um castelo de cartas – tijolo por tijolo, fórmula por fórmula.
E o melhor? No final, você terá exemplos prontos para imprimir, para consultar sempre que precisar!
Introdução ao Cálculo de Área, Perímetro e Volume
O cálculo de área, perímetro e volume é fundamental em diversas áreas do conhecimento, especialmente na engenharia, arquitetura, construção civil e design. A compreensão desses conceitos permite a resolução de problemas práticos relacionados à medição de espaços, à estimativa de materiais e à otimização de projetos. A precisão nesses cálculos é crucial para garantir a eficiência e a segurança das construções e projetos.
Área representa a superfície de uma figura bidimensional, medida em unidades quadradas (m²). Perímetro é a medida do contorno de uma figura bidimensional, expresso em unidades de comprimento (m). Volume, por sua vez, mede o espaço ocupado por um objeto tridimensional, utilizando unidades cúbicas (m³).
Cálculo de Área de Figuras Geométricas Planas
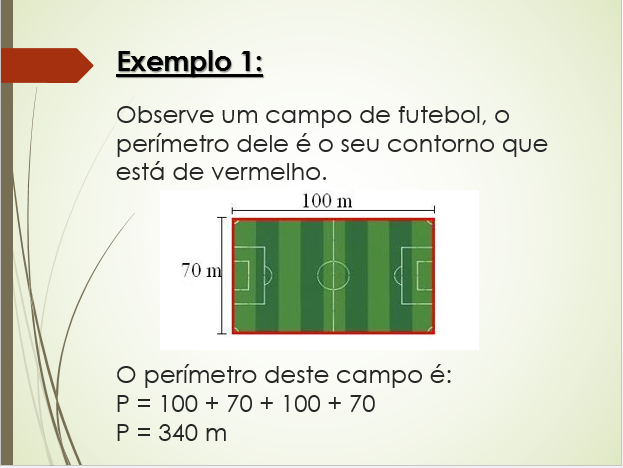
A determinação da área de figuras geométricas planas é essencial em diversas aplicações práticas. Conhecer as fórmulas corretas e aplicá-las corretamente garante a precisão dos cálculos. As fórmulas a seguir demonstram como calcular a área das figuras geométricas planas mais comuns.
| Figura | Fórmula | Exemplo | Resultado |
|---|---|---|---|
| Quadrado | A = l² (lado ao quadrado) | l = 5m; A = 5² = 25 m² | 25 m² |
| Retângulo | A = b x h (base x altura) | b = 4m, h = 6m; A = 4 x 6 = 24 m² | 24 m² |
| Triângulo | A = (b x h)/2 (base x altura / 2) | b = 8m, h = 3m; A = (8 x 3)/2 = 12 m² | 12 m² |
| Círculo | A = πr² (pi x raio²) | r = 2m; A = π x 2² ≈ 12,57 m² | ≈ 12,57 m² |
Exemplo prático: Um terreno retangular mede 15 metros de comprimento e 10 metros de largura. Qual a sua área? Resolução: A = b x h = 15m x 10m = 150 m².
Cálculo de Perímetro de Figuras Geométricas Planas
O perímetro de uma figura geométrica plana representa a soma de todos os seus lados. Seu cálculo é importante para diversas aplicações, como a determinação da quantidade de material necessário para cercar um terreno ou construir uma cerca.
- Quadrado: P = 4l (4 x lado)
- Retângulo: P = 2(b + h) (2 x (base + altura))
- Triângulo: P = a + b + c (soma dos lados)
- Círculo: P = 2πr (2 x pi x raio)
Exemplo: Um quadrado com lado de 3m tem perímetro de 12m (4 x 3m). Um círculo com raio de 2m tem perímetro de aproximadamente 12,57m (2 x π x 2m).
Comparação: Um quadrado com área de 16m² (lado = 4m) tem perímetro de 16m. Um círculo com área de aproximadamente 16m² (raio ≈ 2,26m) tem perímetro de aproximadamente 14,21m. Note que, apesar de possuírem áreas semelhantes, os perímetros diferem.
Cálculo de Volume de Sólidos Geométricos
O cálculo de volume é crucial para determinar a capacidade de recipientes, o espaço ocupado por objetos tridimensionais e a quantidade de material necessário para construir estruturas. A seguir, apresentamos as fórmulas para o cálculo do volume de alguns sólidos geométricos.
| Sólido | Fórmula | Exemplo | Resultado |
|---|---|---|---|
| Cubo | V = a³ (aresta ao cubo) | a = 3m; V = 3³ = 27 m³ | 27 m³ |
| Paralelepípedo | V = l x c x a (comprimento x largura x altura) | l = 5m, c = 2m, a = 4m; V = 5 x 2 x 4 = 40 m³ | 40 m³ |
| Cilindro | V = πr²h (pi x raio² x altura) | r = 2m, h = 5m; V = π x 2² x 5 ≈ 62,83 m³ | ≈ 62,83 m³ |
Exemplo de sólido composto: Uma caixa com dimensões internas de 10m x 5m x 3m possui um furo cilíndrico com raio de 1m e altura de 3m. O volume da caixa sem o furo é 150 m³. O volume do furo é aproximadamente 9,42 m³. O volume final da caixa é aproximadamente 140,58 m³ (150m³
-9,42m³).
Exemplos para Imprimir: Aplicações Práticas
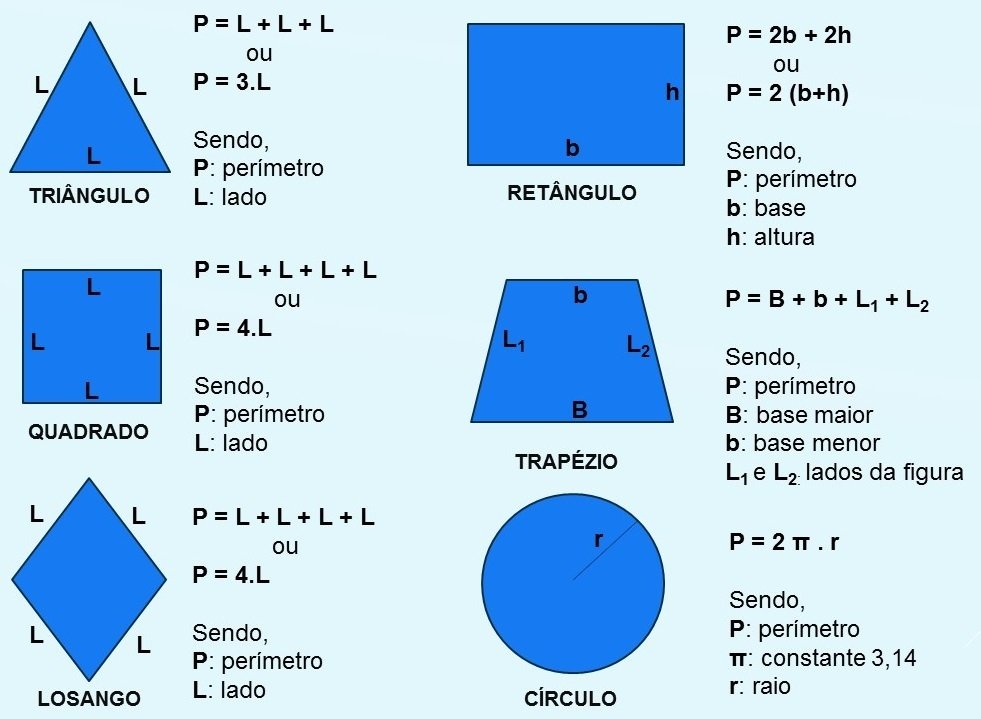
O cálculo de área, perímetro e volume é aplicado em diversas situações do dia a dia. A seguir, alguns exemplos práticos.
Pintura de Paredes: Para pintar as paredes de uma sala, precisamos calcular a área das paredes para estimar a quantidade de tinta necessária. Se a sala tem 4 paredes com dimensões de 3m x 2,5m cada, a área total é 30 m². Considerando uma cobertura de 10 m² por litro de tinta, seriam necessários 3 litros de tinta.
Construção de um Jardim: Para construir um jardim retangular de 5m x 3m, precisamos calcular a área (15m²) para determinar a quantidade de terra e plantas necessárias. O perímetro (16m) indica a quantidade de cerca necessária para delimitar o jardim.
Cálculo da Capacidade de um Tanque: Para determinar a capacidade de um tanque cilíndrico com raio de 1m e altura de 2m, calculamos o volume (aproximadamente 6,28 m³). Como 1 m³ equivale a 1000 litros, a capacidade do tanque é aproximadamente 6280 litros.
Ilustrações Descritivas: Calculo De Area Perimetro E Volume Com Exemplo Para Imprimir
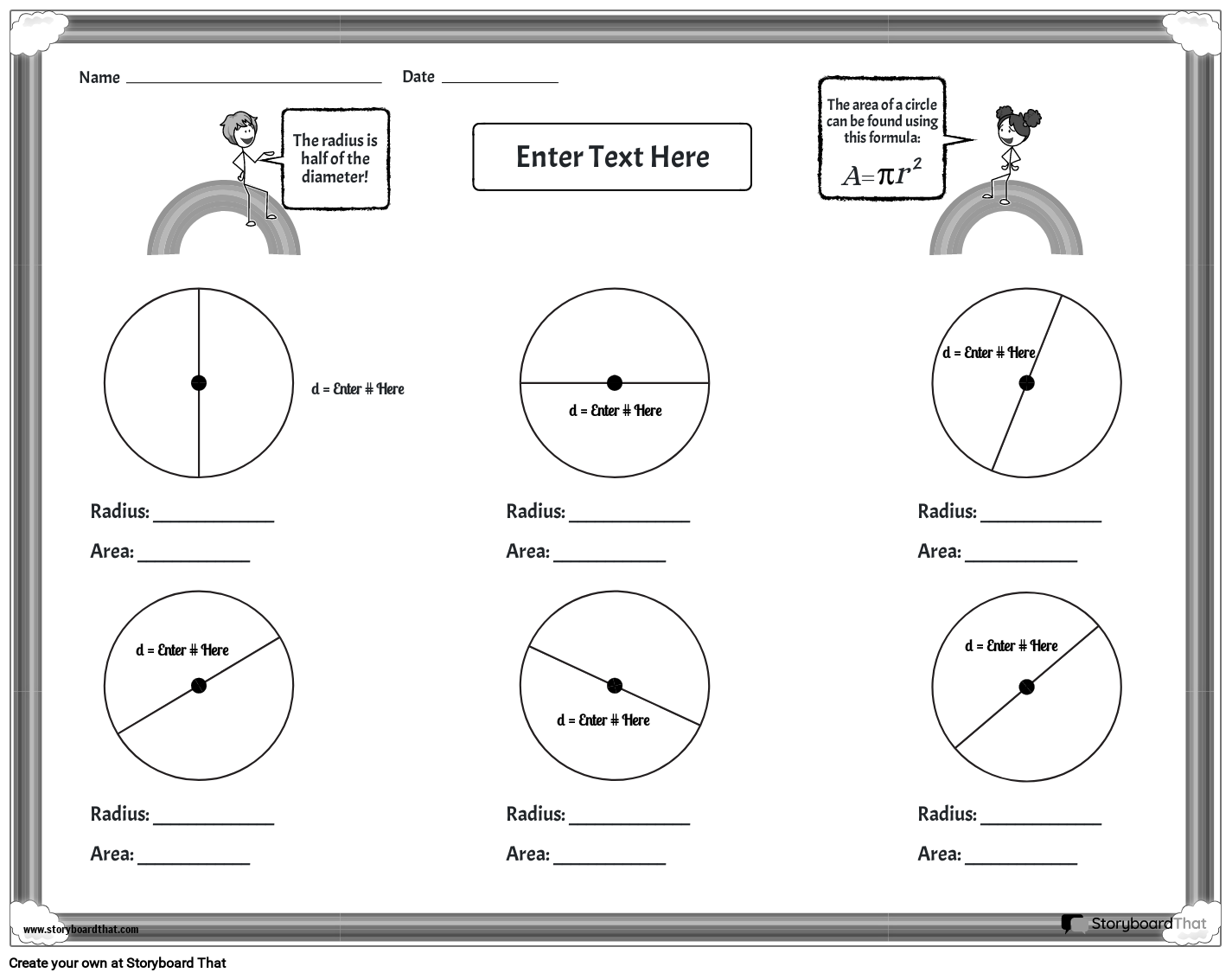
Triângulo Escaleno: Um triângulo escaleno possui três lados de comprimentos diferentes. Considere um triângulo com lados medindo 5cm, 7cm e 9cm. Os ângulos internos também serão diferentes, sendo que a soma dos três ângulos internos sempre resultará em 180 graus. A altura do triângulo variará dependendo do lado escolhido como base.
Prisma Hexagonal: Um prisma hexagonal é um sólido geométrico com duas bases hexagonais congruentes e paralelas, conectadas por seis faces retangulares. Imagine um prisma com bases hexagonais regulares com lado de 4cm e altura de 10cm. Ele possui 12 arestas, 8 vértices e 8 faces (6 retangulares e 2 hexagonais).

